GuidaEsercizi

Operatori logici (parte 1)

• $\neg P$ = “Non P”

• $P\vee Q$ = “P o Q”

• $P\wedge Q$ = “P e Q”

• $P\Rightarrow Q$ = “se P allora Q”

• $P\iff Q$ = P se e solo se Q

• $P_1$ ∧ $P_2$ è soddisfacibile

• $P_2$ ∨ ¬$P_2$ è tautologia

• $P_2$ ∧ ¬$P_2$ è insoddisfacibile

Altre equivalenze logiche utili durante gli esercizi:

• $\neg (\neg p)\equiv p$
• $p\iff q\equiv (p\Rightarrow q)\wedge (q\Rightarrow p)$ (eliminazione della doppia implicazione)
• $p\Rightarrow q\equiv \neg p\vee q$ (eliminazione dell’implicazione)
• $p\wedge (q\vee r)\equiv (p\wedge q)\vee (p\wedge r)$ distributività della congiunzione sulla disgiunzione
• $p\vee (q\wedge r)\equiv (p\vee q)\wedge (p\vee r)$ distributività della disgiunzione sulla congiunzione
• $\neg (p\vee q)\equiv \neg p\wedge \neg q$ ovvero, la negazione della disgiunzione è equivalente alla congiunzione delle negazioni (seconda legge di De Morgan)
• $\neg (p\wedge q)\equiv \neg p\vee \neg q$ ovvero, la negazione della congiunzione è equivalente alla disgiunzione delle negazioni (seconda legge di De Morgan)

Esercizio Data una formula generica creare la tabella di verità $(P\vee Q)\vee (\neg P\wedge Q)$

P	Q	P ∨ Q	¬P ∧ Q	(P ∨ Q) ∨ (¬P ∧ Q)
0	0	0	0	0
0	1	1	1	1
1	0	1	0	1
1	1	1	0	1
Esercizio:
Data una formula generica trasformare in DNF o CNF [[Uni/Primo anno/strutture-discrete/FileRielaborazioni/Tips#come-trasformare-una-qualsiasi-formula-in-cnf-e-dnf		Esempi di come fare]]
Esercizio:
Data una formula dimostrare se è vera:
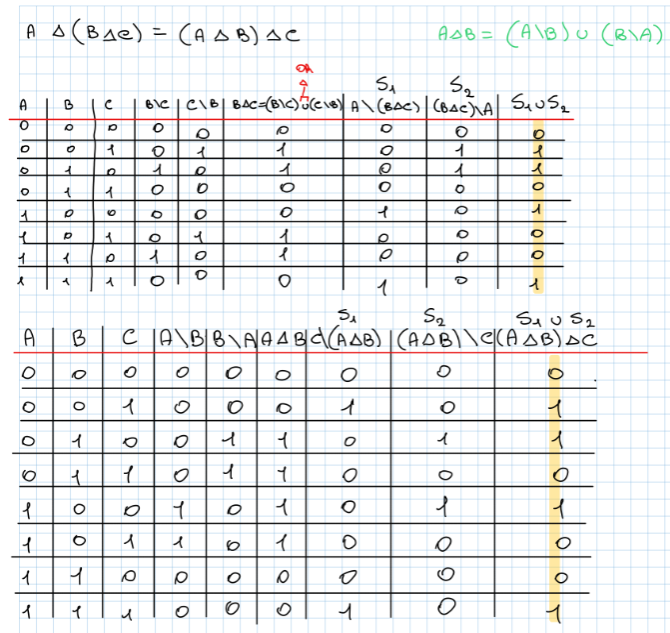Le colonne evidenziate sono uguali quindi l’equivalenza è stata dimostrata.
Di seguito una tabella con delle cose utili per le dimostrazioni di questo tipo:

Scritta matematicamente	Scritta logicamente
$A^C$	$\neg A$
$A\cup B$	$A\vee B$
$A\cap B$	$A\wedge B$
$(A\setminus B)$	$(A\wedge \neg B)$
$A△B=(A\setminus B)\cup (B\setminus A)$	$(A△B)\equiv (A\wedge \neg B)\vee (B\wedge \neg A)$
$A△B=(A\setminus B)\cup (B\setminus A)$ equivale ad uno XOR

Aritmetica modulare (parte 2)

Come calcolare i moduli

Con q indichiamo il quoziente Con r indichiamo il resto

---

+n mod +m Quando sia n che m sono positivi si fa così:

• Dividi n per m.
• Prendi il resto della divisione Esempio: $12\mathrm{mod}5=12/5=2(q)\to 2\times 5=10\to 12-10=2$(r)

---

-n mod +m Quando n è negativo e m è positivo, si fa così:

• Dividi −n per m.
• Trova il resto, ma assicurati che il risultato sia positivo. Se il resto è negativo, aggiungi m per renderlo positivo. Esempio: $-17\mathrm{mod}2=-17/2=-8(q)\to -8\times 2=-16$ (dal -16 al -17 ci sta -1, ma dato che r è negativo sommo m) $\to -1+2=1$(r)

---

+n mod -m Quando n è positivo e m è negativo, il calcolo segue la stessa logica di +n mod +m, ma tenendo presente che il risultato del modulo con un divisore negativo sarà negativo, per convenzione. Esempio: $13\mathrm{mod}-4=13/-4=-3(q)\to (-3)\times (-4)=-12\to 13-12=1(r)$

---

-n mod -m Quando sia n che m sono negativi, il calcolo del modulo segue una logica simile a quella con due numeri positivi, ma il risultato finale sarà negativo per convenzione. Esempio: $-13\mathrm{mod}-4=+3(q)\to 3\times (-4)=-12\to -13-(-12)=-1(r)$

---

Se $n$ è più piccolo di $m$ il risultato è uguale ad $n$ Esempio: $5\mathrm{mod}8=5$

Criteri di divisibilità (parte 2)

Divisibilità per 2: un numero è divisibile per $2$ se è pari

• 4 è divisibile per 2

---

Divisibilità per 3: un numero è divisibile per $3$ se la somma delle sue cifre è un numero divisibile per $3$

• 81 = 8 + 1 = 9 è divisibile per 3

---

Divisibilità per 5: un numero è divisibile per $5$ se l’ultima cifra è $0$ o $5$

• 105 è divisibile per 5

---

Divisibilità per 7: un numero è divisibile per $7$ se $q-2r$ è divisibile per $7$

• $q=$ quoziente della divisione con 10
• $r=$ resto della divisione con 10
• $161:16-2\ast 1=14$ che è divisibile per 7

---

Divisibilità per 9: un numero $n$ è divisibile per $9$ se la sua radice numerica è divisibile per 9, oppure se $n-\rho (n)$ è divisibile per 9.

• $198:1+9+8=18\to 1+8=9$ e quindi 198 è divisibile per 9

---

Divisibilità per altri numeri Per gli altri numeri primi vale la stessa regola del $7$ solo che cambia il numero con cui moltiplichiamo il resto.

TIP

La formula generica per controllare se un numero è divisibile per $p$ è:
$q+a\cdot r$ (con $p$ ed $a$ da questa tabella)

p	a
7	-2
13	4
17	-5
19	2
23	7
11	-1

• $13$ divide $n$ se $q+4r$ è divisibile per $13$
• $17$ divide n se $q-5r$ è divisibile per $17$
• $19$ divide n se $q+2r$ è divisibile per $19$
• $23$ divide n se $q+7r$ è divisibile per $23$
• $11$ divide n se $q-r$ è divisibile per $11$ Esempio di esercizio completo qui: Esempi qui

Inverso modulare (parte 2)

Calcolo della phi:

1. Per n numero primo allora $\phi (n)=n-1$
   • Esempio: $\phi (11)=11-1=10$
2. Con n multiplo di un numero primo φ(n) = $n^{k_1}$ - $n^{k_2-1}$
   • Esempio: φ(16) = $2^4$ - $2^3$
3. Con n prodotto di numeri primi $\phi (n)=\phi (k)\times \phi (q)...$ ($k$ e $q$ sono numeri primi)
   • Esempio: $\phi (10)=\phi (2\times 5)=(2-1)\cdot (5-1)=1\cdot 4=4$

Inverso modulare

Per poter fare l’inverso modulare dobbiamo prima verificare che i due numeri siano comprimi. Dopo aver fatto ciò usi questa formula per calcolarlo:

Formula generica

$(n\mathrm{mod}m{)}^{\phi (m)-1}\mathrm{mod}m$

Esempio:

Calcolo combinatorio (parte 3)

---

Regola somma: se vogliamo contare il numero di elementi dell’unione tra due insiemi ci basta sommare la cardinalità dei due insiemi.

---

Regola prodotto: se vogliamo contare quanti sono le possibili coppie di elementi, il primo scelto da $A$ e il secondo da $B$ ci basta fare $|A|\ast |B|$.

---

Disposizioni e combinazioni

---

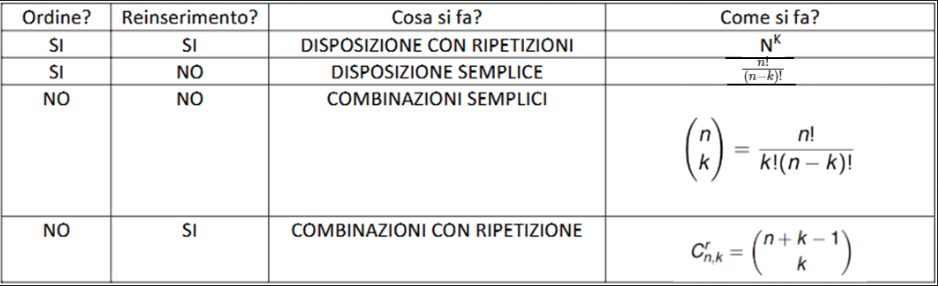
Pigeonhole Principle Il Pigeonhole Principle afferma che se dobbiamo fare entrare $n+1$ piccioni in una piccionaia che contiene $n$ cassette, allora almeno una cassetta dovrà contenere più di un piccione. In generale se abbiamo $n=km+1$ oggetti da sistemare in m contenitori, allora almeno un contenitore dovrà contenere $k+1$ oggetti.

---

Probabilità discrete (parte 3)

---

Assiomi della probabilità:

1. $0\le P(A)\le 1$
   • la probabilità di un evento è sempre compresa tra 1 e 0
2. $P(S)=1$ e $P(\varnothing )=0$
   • la probabilità che un qualsiasi evento campione accada è 1, La probabilità dell’evento impossibile è uguale a zero
3. $P(A\cup B)=P(A)+P(B)-P(A\cap B)$

---

Formula generale della probabilità: $P(A)=\frac{casifavorevoli}{casitotali}$ con $P(A)$ facciamo riferimento alla probabilità che l’evento $A$ accada

---

Formula probabilità condizionata: $P(A|B)=\frac{P(A\cap B)}{P(B)}$ con $P(A|B)$ facciamo riferimento alla probabilità che un’evento $A$ si verifichi dato un’evento $B$ già verificato

---

Regola di Bayes: $P(B|A)=\frac{P(A|B)\ast P(B)}{P(A)}$ con $P(B|A)$ facciamo riferimento alla probabilità che un’evento $B$ si verifichi dato un’evento $A$ già verificato

---

Formula per il calcolo del valore atteso: $E[X]={\sum }_{x}x\cdot P[X=x]$ Dove:

• $x$ è un possibile valore che la variabile casuale $X$ può assumere.
• $P[X=x]$ è la probabilità che $\ast \ast X\ast \ast$ assuma il valore $x$.

Lancio di un Dado

Nel caso del lancio di un dado, la variabile casuale $X$ rappresenta il numero che appare sulla faccia del dado. I possibili valori di $X$ sono 1, 2, 3, 4, 5, e 6, e ognuno ha una probabilità di $\frac{1}{6}$ di verificarsi, perché il dado è equilibrato. Per calcolare il valore atteso $E[X]$: $E[X]=1\cdot P[X=1]+2\cdot P[X=2]+3\cdot P[X=3]+4\cdot P[X=4]+5\cdot P[X=5]+6\cdot P[X=6]$ Poiché la probabilità di ciascun numero è $\frac{1}{6}$, otteniamo:

• $E[X]=1\cdot \frac{1}{6}+2\cdot \frac{1}{6}+3\cdot \frac{1}{6}+4\cdot \frac{1}{6}+5\cdot \frac{1}{6}+6\cdot \frac{1}{6}$ Semplificando, otteniamo:
• $E[X]=\frac{1+2+3+4+5+6}{6}=\frac{21}{6}=3.5$ Quindi, il valore atteso del lancio di un dado è 3.5. Questo significa che, in media, se lanci un dado un numero molto grande di volte, il valore medio dei risultati sarà 3.5.